Pascal's triangle in Ruby for fun

The other day I came across a blog post talking about the Pascal’s triangle and all of it’s interesting properties and I thought it would be fun to implement it using Ruby.

The Pascal’s triangle is a triangular array of the binomial coefficients, but you don’t have to calculate them in order to create the triangle because each row can be constructed using the previous one, like this:

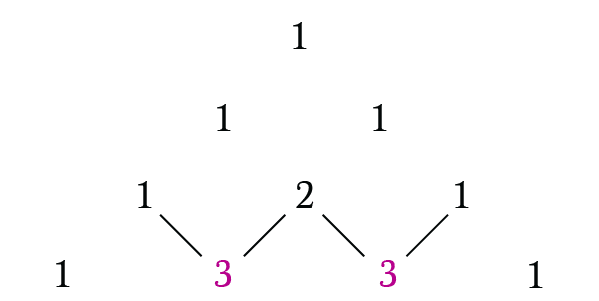
Forming something like this:

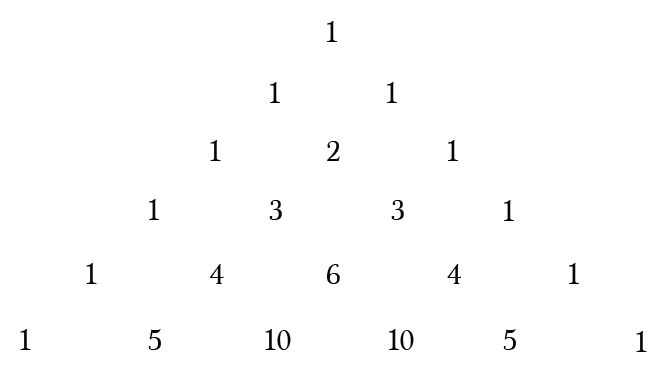
What amazes me is that this simple construction can be used to calculate a lot of interesting things. Even though there are more efficient ways to do the same calculations I thought it’d be fun to do it this way.

Pascal’s triangle itself

First, we are going to need something that calculates the triangle, let’s create a class for this:

class PascalTriangle
  def initialize
    @triangle = [[1]]
  end

  def get_file(param)
    return @triangle[param] if @triangle[param]

    previous_file = get_file(param - 1)
    @triangle << calculate_new(previous_file)

    @triangle[param]
  end

  private

  def calculate_new(previous_file)
    current_file = [1]
    (0..(previous_file.size - 1)).each do |idx|
      next if idx == previous_file.size - 1

      current_file << previous_file[idx] + previous_file[idx + 1]
    end
    current_file << 1

    current_file
  end
end

I used a recursive function to create each row when needed and dynamic programming to store the intermediate results to make it faster for successive calls.

Fibonacci

Let’s start with my favourite application of the triangle, the Fibonacci sequence. Basically you can get the elements of the sequence doing:

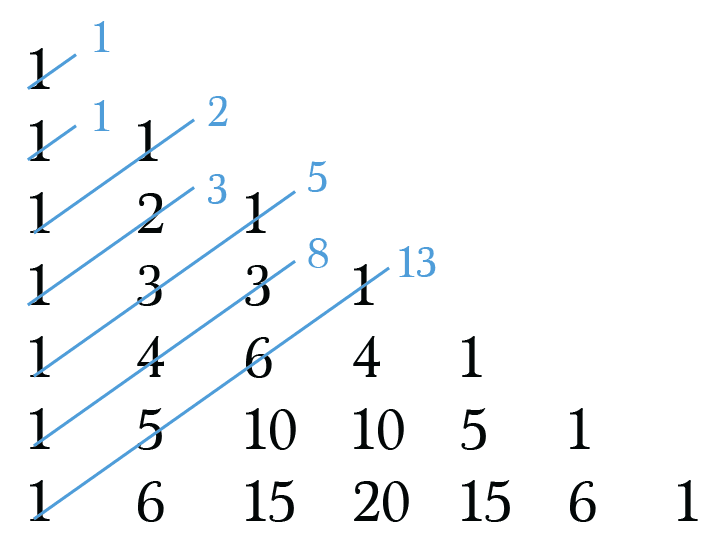
We can implement a method like this:

@triangle = PascalTriangle.new

def fibonacci(n)
  return 0 if n <= 1
  return 1 if n == 2

  result = 0
  (0..n).reverse_each.with_index do |n, idx|
    coefficients = @triangle.get_file(n - 2)
    next unless coefficients[idx]

    result += coefficients[idx]
  end
  result
end

(1..20).map { |n| fibonacci(n) } #=> [0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181]

Binomial coefficient

Each element of the triangle corresponds to a binomial coefficient:

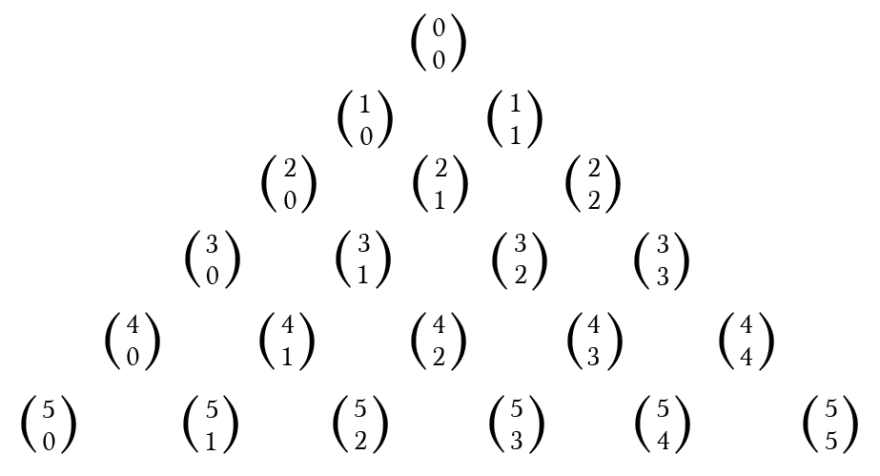
So it’s super easy to get the value:

def binomial_coefficient(n, k)
  file = @triangle.get_file(n)
  file[k]
end

Binomial expansions

Coefficients of the expansion of a binomial raised to a positive integer N appear in the Nth row of the Pascal’s triangle:

(x + y)^2 = x^2 + 2xy + y^2 = 1*x^2 + 2*xy + 1*y^2

With this not only wee can get the coefficients, but calculate (x+y)^n:

def binomial_power(a, b, n)
  coefficients = @triangle.get_file(n)

  result = 0
  coefficients.each_with_index do |coefficient, idx|
    result += coefficient * a**(n - idx) * b**idx
  end

  result
end

Powers of 2

If we sum each number of the Nth row of the triangle we get 2^n!

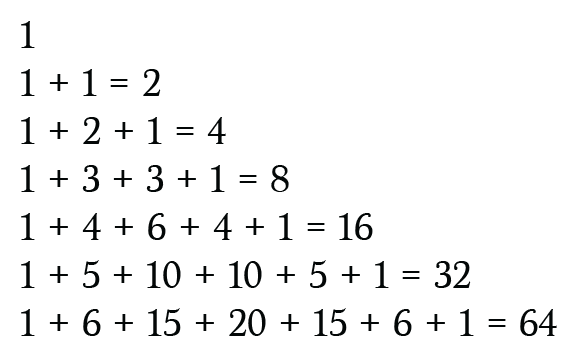
def power_of_2(n)
  coefficients = @triangle.get_file(n)
  coefficients.sum
end

Powers of 11

Here is a more complicated one. We can build the powers of 11 concatenating each number of a row.

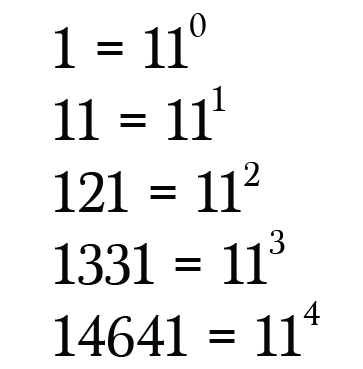
Things get more complicated when the numbers start to get bigger. So we need to carry the tens place over to the number on it’s left:

def power_of_11(param)
  coefficients = @triangle.get_file(param)

  if param <= 4
    coefficients.join.to_i
  else
    coefficients_with_carry = [0]
    coefficients.reverse_each.with_index do |coefficient, idx|
      coefficient_with_carry = coefficient + coefficients_with_carry[idx]

      if coefficient_with_carry < 10
        coefficients_with_carry[idx] = coefficient_with_carry
        coefficients_with_carry[idx + 1] = 0
      else
        coefficients_with_carry[idx] = coefficient_with_carry % 10
        coefficients_with_carry[idx + 1] = (coefficient_with_carry / 10.0).floor
      end
    end
    coefficients_with_carry.reverse.join.to_i
  end
end

Series

We can find some series of numbers in the triangle

Perfect squares

Perfect squares are numbers that can be expressed as the product of two equal integers, for example 4 is a perfect square becase you can express it like 2^2 = 4. The perfect squares are found in the third column of the triangle, the trick is that you have to sum the element of the previous row:

We can create a class that returns all of the perfect squares one by one:

class PerfectSquaresSeries
  def initialize(triangle)
    @triangle = triangle
    @current_file = 3
  end

  def next
    previous_file = @triangle.get_file(@current_file - 1)
    file = @triangle.get_file(@current_file)
    @current_file += 1

    file[2] + previous_file[2]
  end
end

series = PerfectSquaresSeries.new(@triangle)
series.next #=> 4
series.next #=> 9
series.next #=> 16
series.next #=> 25
series.next #=> 36
series.next #=> 49
series.next #=> 64
series.next #=> 81

Natural numbers

If we take a look at the second column we see that the natural numbers appear:

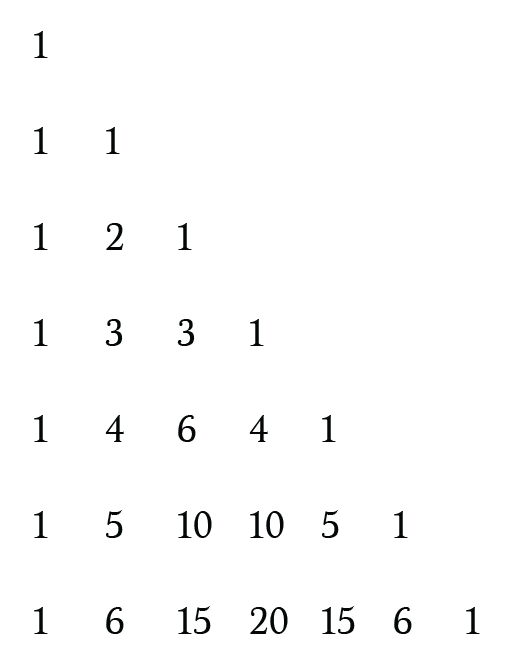
This is not something very interesting, but if we see the succesive columns we observe the triangular, tetrahedral, pentalope numbers and so on (which I generalized calling them the N-hedral numbers).

N-hedral numbers

All the series can be found in the Nth column of the triangle, and we can get them like this:

class NHedralSeries
  def initialize(triangle, n)
    @triangle = triangle
    @current_file = n - 1
    @n = n
  end

  def next
    file = @triangle.get_file(@current_file)
    @current_file += 1
    file[@n - 1]
  end
end

natural = NHedralSeries.new(@triangle, 2)
(0..10).map { natural.next } #=> [1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11]

triangular = NHedralSeries.new(@triangle, 3)
(0..10).map { triangular.next } #=> [1, 3, 6, 10, 15, 21, 28, 36, 45, 55, 66]

tetrahedral = NHedralSeries.new(@triangle, 4)
(0..10).map { tetrahedral.next } #=> [1, 4, 10, 20, 35, 56, 84, 120, 165, 220, 286]

pentalope = NHedralSeries.new(@triangle, 5)
(0..10).map { pentalope.next } #=> [1, 5, 15, 35, 70, 126, 210, 330, 495, 715, 1001]

I hope you enjoyed this exercise as much as I did! You can find my complete implementation here.

Buy me a coffee